电力科普丨串联谐振电路

发布日期：2020-06-01　点击：3276次

湖北四方国瑞电力控股有限公司是一家专业研发生产串联谐振的厂家，本公司生产的串联谐振设备在行业内都广受好评，以打造最具权威的“串联谐振“高压设备供应商而努力。

谐振变压器的基本公式就是ω=1/√（LC），其中ω是电源的角频率=2лf，L和C是负载或设备的电感和电容量。要完全满足等式，ω、L、C中至少需要有一个参数是可调的，为了满足输出电压或电流的要求，L和C中必须有一个是可调的，为了精确找到谐振点，还需要参数可以无级微调。所以，现代谐振变压器一般使用变频电源作为电源，以便调整ω，以带抽头电抗器作为L，与C配合就可以方便地找到谐振点。

高频谐振变压器是作为开关电源最主要的组成部分。开关电源一般采用半桥式功率转换电路，工作时两个开关三极管轮流导通来产生100kHz的高频脉冲波，然后通过高频变压器进行降压，输出低电压的交流电，高频变压器各个绕组线圈的匝数比例则决定了输出电压的多少。

  在研究各种谐振电路时，常常涉及到电路的品质因素Q值的问题，那末什么是Q值呢？下面我们作详细的论述。

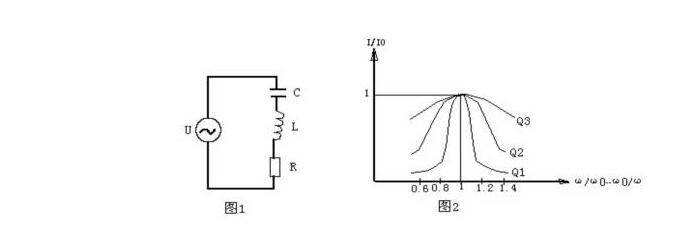
   图1是一串联谐振电路，它由电容C、电感L和由电容的漏电阻与电感的线电阻R所组成。此电路的复数阻抗Z为三个 元件的复数阻抗之和。

Z=R+jωL+(-j/ωC)=R+j(ωL-1/ωC)  ⑴

   上式电阻R是复数的实部，感抗与容抗之差是复数的虚部，虚部我们称之为电抗用X表示, ω是外加信号的角频率。

 当X=0时，电路处于谐振状态,此时感抗和容抗相互抵消了，即式⑴中的虚部为零，于是电路中的阻抗最小。因此电流最大，电路此时是一个纯电阻性负载电路，电路中的电压与电流同相。电路在谐振时容抗等于感抗，所以电容和电感上两端的电压有效值必然相等，电容上的电压有效值UC=I*1/ωC=U/ωCR=QU，品质因素Q=1/ωCR，这里I是电路的总电流。

    电感上的电压有效值UL=ωLI=ωL*U/R=QU品质因素Q=ωL/R

  因为：UC=UL  所以Q=1/ωCR=ωL/R

  电容上的电压与外加信号电压U之比UC/U= （I*1/ωC）/RI=1/ωCR=Q

  电感上的电压与外加信号电压U之比UL/U= ωLI/RI=ωL/R=Q

  从上面分析可见，电路的品质因素越高，电感或电容上的电压比外加电压越高。

  电路的选择性：图1电路的总电流I=U/Z=U/[R2+(ωL-1/ωC)2]1/2=U/[R2+(ωLω0/ω0-ω0/ωCω0)2]1/2  

  ω0是电路谐振时的角频率。当电路谐振时有：

ω0L=1/ω0C

  所以I=U/{R2+[ω0L(ω/ω0-ω0/ω)]2}1/2= U/{R2+[R2(ω0L/R)2](ω/ω0-ω0/ω)2}1/2= U/R[1+Q2(ω/ω0-ω0/ω)2]1/2

  因为电路谐振时电路的总电流I0=U/R，

  所以I=I0/[1+Q2(ω/ω0-ω0/ω)2]1/2有：I/I0=1/[1+Q2(ω/ω0-ω0/ω)2]1/2作此式的函数曲线。设(ω/ω0-ω0/ω)2=Y

  曲线如图2所示。这里有三条曲线，对应三个不同的Q值，其中有Q1>Q2>Q3。从图中可看出当外加信号频率ω偏离电路的谐振频率ω0时，I/I0均小于1。Q值越高在一定的频偏下电流下降得越快，其谐振曲线越尖锐。也就是说电路的选择性是由电路的品质因素Q所决定的，Q值越高选择性越好。